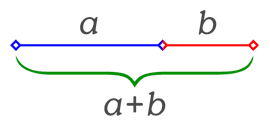
¿Cómo hacerlo entonces? Vamos a empezar hablando primero de la razón aurea, de phi. Phi es un número irracional que nace de la idea de dividir un segmento (fig1) de modo que la longitud a+b sea a, como a es al segmento b. En la wikipedia teneis el desarrollo matemático explicado, en el que no me voy a centrar en este blog, sobre con decir que finalmente
Estareis pensando -Bueno, esto es muy bonito, sí, pero que tiene que ver esto con el arte, la fotografía, la composición... -pues en realidad mucho más de lo que puedas pensar. Leonardo Fibonacci descubrió en el siglo XII la famosa serie numérica que lleva su nombre, la serie de Fibonacci, que comenzando por 0 y por 1, construye el resto de sus términos de forma que an = an-1 + an-2 , es decir, cada término se obtiene sumando los dos términos anteriores:
8/5 = 1.600
13/8 = 1.625
...
144/89 = 1,6179775280898876404494382022472
Desde en la concha de un Nautilus, que "crece" siguiendo la serie de Fibonacci y manteniendo una proporción próxima a la aurea, hasta las tormentas:

Pasando por... nosotros mismos:

Fig 4. Proporciones aureas en el hombre - Imagen esta web.
Vale, ahora que he conseguido que veas números por todas partes, ¿qué tiene que ver esto con la fotografía? Seguro que muchos conoceis la regla de los tercios o de los puntos fuertes
Fig 5. Regla de los tercios
La regla de los tercios es una conocida regla en fotografía que nos indica como disponer los elementos clave en una imagen. Dividiendo el fotograma de la forma que se ve en la imagen 5, los puntos de corte de las lineas divisorias suponen los puntos clave de la imagen, donde el observador centrará su atención. Lo que no tantos saben es de donde viene esta regla. Al parecer no solo Phi está por todas partes, sino que además nos resulta visualmente atractivo, por lo que se utiliza generalmente en arquitectura, fotografía e incluso en música. Veamos que pasa si dividimos un cuadro en rectangulos aureos sucesivamente:

Fig6. Rectángulos aureos - Imagen DivulgaMAT
En la figura se representan dichos rectángulos y la espiral que se obtiene a partir de ellos. ¿Veis donde está situado el centro de la espiral? Veamos la siguiente imagen superpuesta varias veces pero girada:
Fig6. Origen de la regla de los tercios
¡Vaya! Si os fijais, las espirales convergen hacia los puntos fuertes. De ahí pues la regla de los tercios: Se trata una regrla rápida para hacer composiciones que respeten las proporciones aureas.
Después de todo este rollo, volvamos a las imagenes de Maria.
Aquí vemos las subdivisiones anteriormente comentadas superpuestas sobre la imagen de María. Como podeis ver, la propia espiral del puente retratado en la imagen ¡está diseñada siguiendo la espiral aurea! Y no es de extrañar, puesto que los arquitectos saben perfectamente que los diseños que cumplen dichas proporciones nos resultan por alguna cuestión más "atractivos". ¿Qué tendría que haber hecho María para que su composición fuera incuestionable? Pues sencillamente debería haber situado el punto de fuga en uno de los puntos fuertes de la imagen:
Este es un recorte de la imagen ajustando el punto de fuga. No se puede apreciar bien el resultado porque estamos cargandonos un pedazo de la imagen, pero se hace evidente que la composición resultante es más armoniosa y que la sensación de profundidad es mucho más notable.
Y por supuesto, para corroborar lo anteriormente dicho de la regla de los tercios, aquí teneis dicha imagen con la regla de los tercios superpuesta.
Solo dar un apunte último a la hora de componer: Las culturas que leen libros de izquierda a derecha y de arriba abajo, también leen las imagenes en dicho orden. Lo mismo sucede para las culturas, como la Árabe, que leen de derecha a izquierda y de arriba a abajo. Es importante entender este orden de lectura a la hora de componer una imagen de modo que aquel que la visualice se encuentre los elementos en el orden que deseamos.









8 comentario(s) - Click para comentar:
increíble sin lugar a dudas!me dejas sin palabras.
el sitio es increíble, pero mi imagen, el punto de fuga.. todo ello esta mal.
muy bien!!
Hola, todo bien, pero la foto al final está corrida para hacer coincidir a los puntor fuertes.
Claro... evidentemente se hace eso y se explica que se hace ese recorte para desplazarla hacia los puntos fuertes.
Hello There. I found your blog using msn. This is an extremely well written
article. I will make sure to bookmark it and return to read more of your useful info.
Thanks for the post. I will certainly return.
Look into my web blog - Http://Www.Crazyteenpics.Com/
Hi, guantanamera121212
I do accept as true with all of the concepts you've presented on your post. They are really convincing and can certainly work. Still, the posts are very brief for starters. Could you please lengthen them a little from next time? Thanks for the post.
My webpage www.porn-selection.com
Publicar un comentario